Computing the boundary complex using Macaulay2

2023-05-08


Suppose you are given a divisor $D$ on a variety $X$, with $D=\cup_{i=0}^N D_i$ the decomposition into its irreducible components. Suppose moreover that the divisor is simple normal crossing, or even combinatorial normal crossing in the sense that all non-empty intersections $D_{i_1}\cap ... \cap D_{i_k}$ have codimension $k$. One can form the boundary complex $\Delta(D)$ of $D$, a simplicial complex on the set $\{0,...,N\}$ recording the intersection properties of the $D_i$. We proceed as follows:

  1. For each $D_i$, add a vertex $[i]$ to the complex $\Delta (D)$.
  2. For each non-empty intersection $D_{i_1} \cap ... \cap D_{i_k}$, add a k-simplex $[i_1,..,i_k]$ between the vertices $[i_1]$, $[i_2]$,... through to $[i_k]$.
From this boundary complex, interesting information about the divisor $D$ and its complement $U:= X\setminus D$ can be deduced.

When working in the projective plane $\mathbb{P}^2$, we might have a divisor $D$ given as the union of curves $D_0,...,D_N$, each given by a corresponding irreducible polynomials $f_i$. Suppose we are given this list of polynomials $f_0,...,f_N.$

Here is some Macaulay2 code that will compute the boundary complex in this case: 


boundaryComplex = method()
boundaryComplex := listOfDivisors -> (
    -- Helper function, takes list of polynomials and determines 
    -- if their intersection is irrelevant ideal
    intersectionIsIrrelevantIdeal = s -> (
        radical(ideal(s)) != ideal(y_0,y_1,y_2)
        );
        -- Select all possible subsets of divisors
        rawPolySubs = subsets(listOfDivisors);
        polySubs = rawPolySubs_{1..(#rawPolySubs-1)};
        -- Create a true/false mask for when this intersection is the irrelevant 
        -- ideal and hence those divisors do not intersect in projective space
        mask = apply(polySubs,intersectionIsIrrelevantIdeal);
        -- List all faces
        R=QQ[x_0..x_(#listOfDivisors-1)];
        -- take subsets of numbers 0 through length(listOfDivisors), then 
        -- drop the first as it is always the empty set
        faceNums = drop(subsets(toList(0..(#listOfDivisors-1))),1); 
        faceSubs = drop(subsets(toList(x_0..x_(#listOfDivisors-1))),1);
        -- Filter by the mask
        faceMonomials = {};
        faceList = {};
        for i in 0..(#faceSubs-1) do (
            if mask#i then (
                faceMonomials=append(faceMonomials,fold((i,j)->i*j, faceSubs#i));
                faceList=append(faceList,faceNums#i);
            )
        );
    (simplicialComplex(faceMonomials),faceList)
)

The function outputs two objects:

  1. First, a SimplicialComplex object, which is exactly $\Delta(D)$, and can be easily visualized (see below).
  2. Second, a list of the faces of this simplicial complex as subsets of the integers $0,..,N$, which can be useful for a quick inspection and building the simplicial complex in some other program, such as Polymake
It should be a straightforward matter to generalize this to divisors on other varieties, say in the toric setting, by changing the irrelevant ideal $(y_0,y_1,y_2)$ on line 6 to another ideal.

An example run of this code is given as follows: 


S = QQ[y_0..y_2]
l0 = y_0
l1 = 2*y_1-y_2+y_0
l2 = y_2
c1 = y_0*y_1 + y_0*(y_2 - y_0) + y_1*(y_2 - y_1)
c2 = y_0*y_1 + y_0*(y_2 - 3*y_0) + 3*y_1*(y_2 - 3*y_1)
listOfDivisors = {l0,l1,l2,c1,c2}

(bc, lf) = boundaryComplex(listOfDivisors)

Moreover, using the Visualize package, we can quite easily visualize two-dimensional simplicial complexes (three-dimensional are per now not supported). In the above example this would proceed as follows: 


loadPackage "Visualize"
openPort("8090")

visualize bc

closePort()
(Remember to close the port after you are done, if you forget, you might need to use lsof -i tcp:8090 and kill the process holding onto the port).

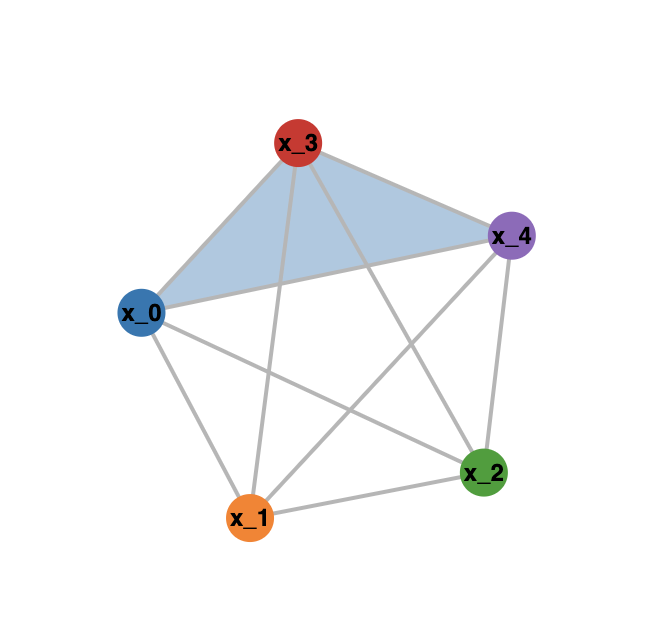
This should give you a nice interactive browser animation, looking similar to the following image: Image of the dual complex

For three-dimensional simplicial complexes, the following code will transform the list lf into a string which can be pasted in polymake to create the corresponding polymake simplicial object: 


facesToPolymakeSimplicialComplex = method()
facesToPolymakeSimplicialComplex := lst -> (
    listStr = toString(lst);
    listStr = replace("{","[",listStr);
    listStr = replace("}","]",listStr);
    out = concatenate({"$s = new SimplicialComplex(INPUT_FACES=>",  listStr, ");"});
    out
)

facesToPolymakeSimplicialComplex(lf)

This can then be visualized using the command $s->VISUAL;

Bibliography: